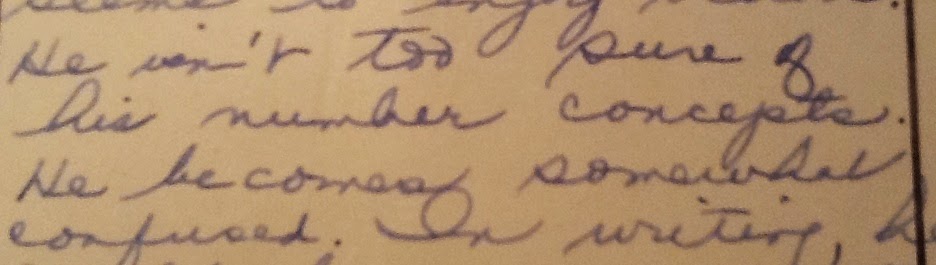 |
| This is from my first grade report card. My parents saved lots of things. |
 |
| I eventually learned how to tell time. |
Things never got better. I never caught up, never caught on, and I suppose this is when my confusion turned to feelings of inadequacy, fear, anxiety, and hostility. Here's a work sample from grade 4:
 |
| 4 out of the 7 problems are marked incorrect with a red "x". How's that for meaningful feedback, Michael Pershan? |
(It's funny what you remember. It must have been in this class that the teacher asked us to put long division problems on the board for our classmates to solve. When it was my turn, I wrote something I supposed would be really difficult, with 99 as the divisor. 99 seemed like a "hard" number to me. The girl who was chosen to solve the problem laughed, "99 is easy to divide. It's close to 100." I didn't get it.)
Again, my math warranted a report card comment:
 |
| The "of course" really stung. This was doubly devastating because I had a crush on Mrs. Hughes. Despite her hopefulness, it didn't improve. |
Justin Lanier's smOOC Math is Personal. It also arises from feelings I have about becoming a more active member of the MTBoS, and connecting with people who come from mathematical backgrounds very different from my own. But what actually got me digging up my old report cards was reading a recent post from Fawn Nguyen, who shared excerpts from a book called The Number Sense, by Stanislas Dehaene. This one jumped right off the page:
… most children enter preschool with a well-developed understanding of approximation and counting. In most math courses, this informal baggage is treated as a handicap rather than as an asset. Finger counting is considered a childish activity that a good education will quickly do away with. How many children try to hide when they count on their fingers because “the teacher said not to”?
Despising children’s precocious abilities can have a disastrous effect on their subsequent opinion of mathematics.
… It seems more likely that many of these “mathematically disabled” children are normally abled pupils who got off to a false start in mathematics. Their initial experience unfortunately convinces them that arithmetic is a purely scholastic affair, with no practical goal and no obvious meaning. They rapidly decide that they will never be able to understand a word about it. The already considerable difficulties posed by arithmetic to any normally constituted brain are thus compounded by an emotional component, a growing anxiety or phobia about mathematics.
So it is ironic that I find myself in my current position, which I suppose goes to show that you really never know where life will lead. And I am now part of a community where sometimes people talk like this...
New on my blog: if m≠1 is rational, can y=mx be tangent to y=sinx? http://t.co/blu5hOQPZl
— Dave Richeson (@divbyzero) August 27, 2014
...and I haven't much of a clue what they're driving at.
But it is that same MTBoS that has made me see that it just doesn't have to be that way, something I describe in My Confession, Part 2.





