0.4 and 0.75
Tell me everything you can about them.
As described here, I've fallen in love with this very simple prompt, and it's how Rich and I decided to kick off a unit on decimals. We followed the previously established protocol, first giving each student time to work on a card individually, then giving them an opportunity to pass their cards around and take notes. Upon receiving their cards back, they could then cross out or add information. When all was said and done, between the AM and PM classes we had 35 five by eight index cards filled with fifth grader thoughts about decimals. Or, as I like to think of it, gold.
But what now? What to do with the cards? We had found a way to uncover all this thinking, but if we didn't use it, capitalize on it somehow, then it would all go to waste. We had opened up a chest, and found treasure inside. Now we had to find a way to spend it.
My idea was to use their thoughts to create an agree/disagree activity. First, I poured through the cards and selected some statements:
Rich and I decided to wait a week or so, long enough for the kids to get some decimal work under their belts. I wanted to hold off on anything to do with operations and focus on place value, fractions, and comparisons. I whittled the list down to five items:
 |
| An embarrassment of riches. Not to mention a low stress formative assessment. |
But what now? What to do with the cards? We had found a way to uncover all this thinking, but if we didn't use it, capitalize on it somehow, then it would all go to waste. We had opened up a chest, and found treasure inside. Now we had to find a way to spend it.
My idea was to use their thoughts to create an agree/disagree activity. First, I poured through the cards and selected some statements:
 |
| On target and misguided, commonly held and unusual. |
- 0.4 is closer to 0 then to 1/2.
- Both 0.4 and 0.75 equal to a fraction with the same denominator.
- 0.4 is 40 because the 4 is in the tenths place.
- In 0.75 the 7 is in the tenths place and the 5 is in the ones place.
- 0.75 is closer to 1 than 0.4.
They could choose agree, disagree, or not sure, and I made certain to give them room on the paper to justify their decisions. We gave them time to work on their answers individually, and then meet with classmates to discuss and, hopefully, argue and hash things out.
As Rich and I circulated around the room, listening in, subtly nudging and facilitating, we found that some statements provoked more discussion and disagreement than others. Those were the ones we decided to highlight in a whole class discussion.
First was the statement that both 0.4 and 0.75 equal to a fraction with the same denominator. I included this one because I wanted to both emphasize the equivalency between 0.4 (4/10) and 0.40 (40/100) and also because I wanted the students to convert the decimals into fractions. These sample responses are illustrative of how I was thinking:
 |
| After first disagreeing, this student changed his mind. |
 |
| Not all students were able to respond. |
A few saw it differently:
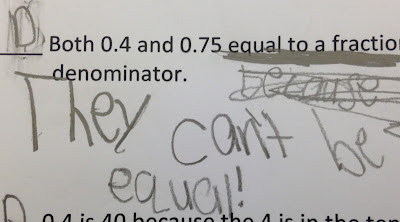 |
| Strongly worded! |
 |
| Well, that's true! |
The following day we tackled this one: 0.4 is 40 because the 4 is in the tenths place. I included this because it had an element of truth (the 4 is in the tenths place) but was inaccurate due to the important distinction between tens and tenths that was still confounding some students.
 |
| This was representative of the agree faction, however it directly contradicts the original statement. |
 |
| I like how this student underlined the th in tenths! |
 |
| This argument convinced the remaining few in the agree camp to change their minds. Money talks. |
Some observations:
- In terms of content, the experience drove home how important SMP 6 (Attend to precision) is when talking about decimals. Minor changes, both to the location of the decimal point and to how we write and talk (tens vs. tenths) have major consequences.
- The activity also provided an opportunity to exercise the SMP 3 muscle: Construct viable arguments and critique the reasoning of others. Pictures and models, like number lines, proved especially effective.
- From start to finish the activity provided a nice balance between individual work, group collaboration, and whole class discussion. The resolution of the disagreement provided a natural context for direct teacher instruction.
Above all, I was gratified that the thoughts collected on the cards didn't go to waste. As I reflected on the experience, I thought about something from my days as a third grade classroom teacher. I had always enjoyed the unit we taught on Native Americans, and remembered how fascinated the kids were studying the Plains Indians tribes and the way they used the buffalo. Meat, bones, hide, hair, tail, hoof, brain, stomach, bladder, intestine; they found practical uses for every part of the animal, even its dung! Were the cards more like the buffalo than like gold? Rather than think of them as currency that we needed to spend, maybe it was more useful to think of them the way the Plains Indians thought about the buffalo, as a natural resource that we could use not only as a formative assessment for determining who knew what and a way to uncover some misconceptions, but for other things as well. Like giving everyone a headache. Like starting an argument in math class. Like providing a reason to get together and talk things through.
Student thinking. A precious natural resource. And it's endlessly renewable!
Student thinking. A precious natural resource. And it's endlessly renewable!





















